|
Since restrictions were eased in Australia, starting on 1 May 2020, the simple model presented here suggests that the efficacy of the restrictions still in place remain above 60%. To keep the effective R0 below 1 the efficacy of restrictions needs to be above 55% (an E of 0.55). E = 1 - R/R0.
0 Comments
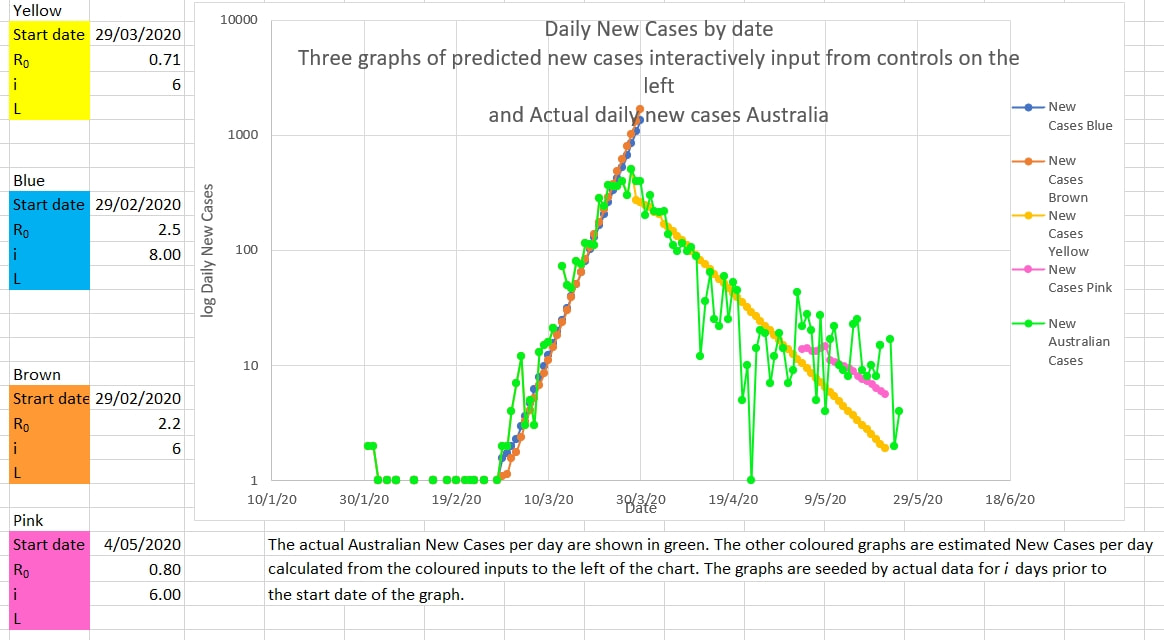
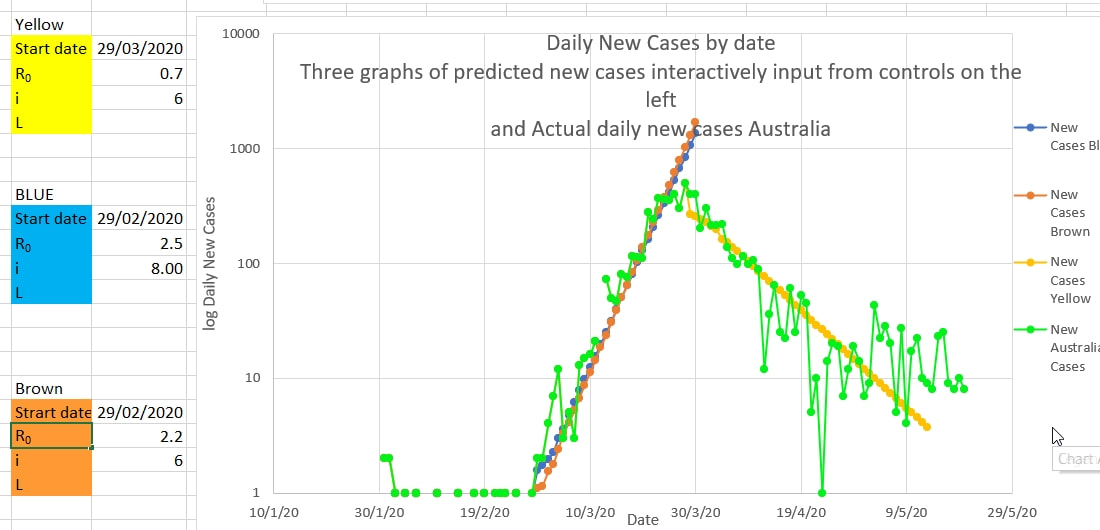
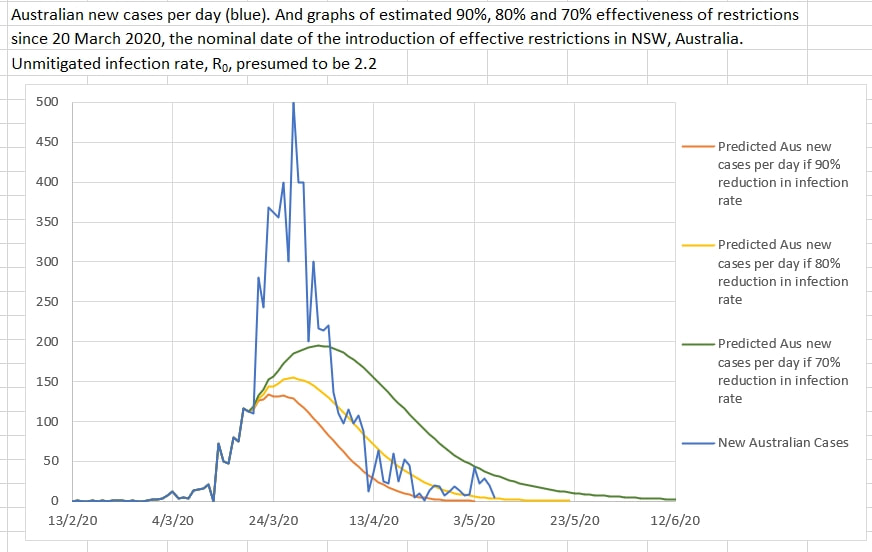
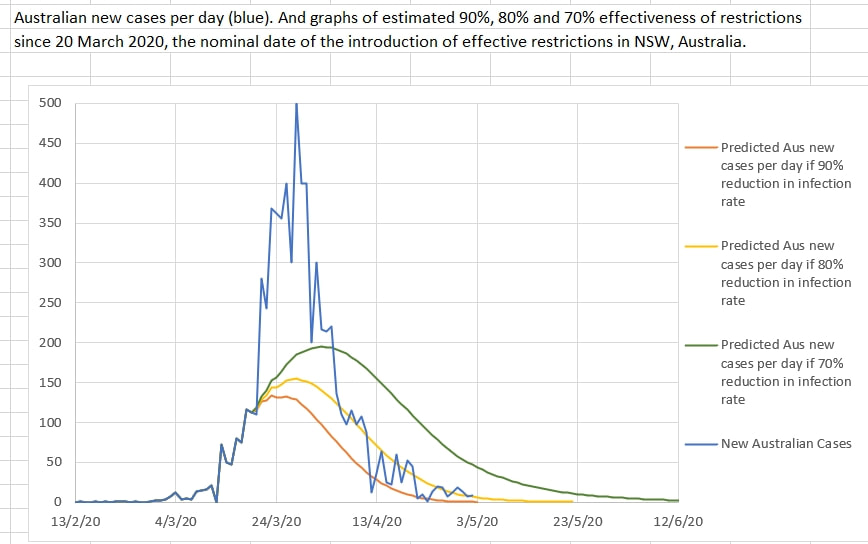
Ro and infection time (i, the time a case remains infectious) are often determined empirically by case tracing and contact tracing in the field. It is usually considered difficult to estimate Ro and i from population data and models, like new and total cases. It does appear that Ro and i can be estimated graphically by plotting curves with various values for Ro and i such that the curves match the actual data of new and total cases. Restrictions were put in place in Australia on 20 March and the maximum new cases a day occurred on 28 March 2020. Ro and i change the slope of log new cases graph in opposite directions, so there are a number of 'sets' of Ro and i which fit the actual data equally well. It may be possible to determine which 'set' of Ro and i best agrees with the empiric field data.
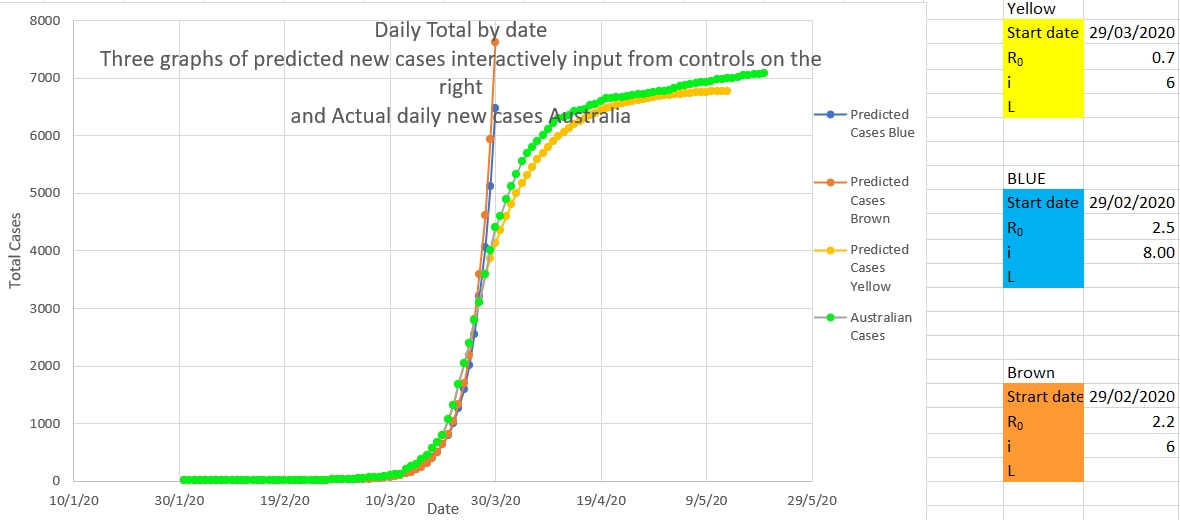
Ro and i produce different shapes in the graph of the total cases near the end of the epidemic. Presumably i should have the same value in both graphs. Then R at this time can be more easily estimated and may suggest the effective R while the restrictions are in place. The efficacy of restrictions appears to be 1- 0.7/2.2 which is 68%. Trump says he is taking hydroxychloroquine because it is a good idea. It seems promising and there is minimal downside.
But it is said - in set theory apparently - that there are a great number of reasonable explanations for any given set of facts. Presumably only one of those reasonable explanations will be true or correct. So the probability that any one reasonable explanation is in fact the true or correct one is close to zero. One correct reasonable explanation and a great many not-correct reasonable explanations. That appears to be why almost all good ideas in medicine are wrong. And in every other field as well. The corollary is well known. Thoroughly test each good idea before accepting it. Double blinded randomised trials are the gold standard in medicine. The FDA and similar organisations require convincing trials before releasing any 'good idea' on the public. It is not a good idea to accept even very good ideas till they have been thoroughly tested. Good ideas are usually wrong. Cluster or single case management. Apparently speed is of the essence. It makes sense because cases are most infectious early, and in a space with more people who stay or meet for longer the Ro is much higher than the quoted 'average' Ro.
https://www.recover-europe.eu/wp-content/uploads/2020/05/Time_is_of_the_essence_15052020.pdf The problem of dealing with isolated cases and clusters of Covid-19 may be a lack of understanding about the meaning of Ro.
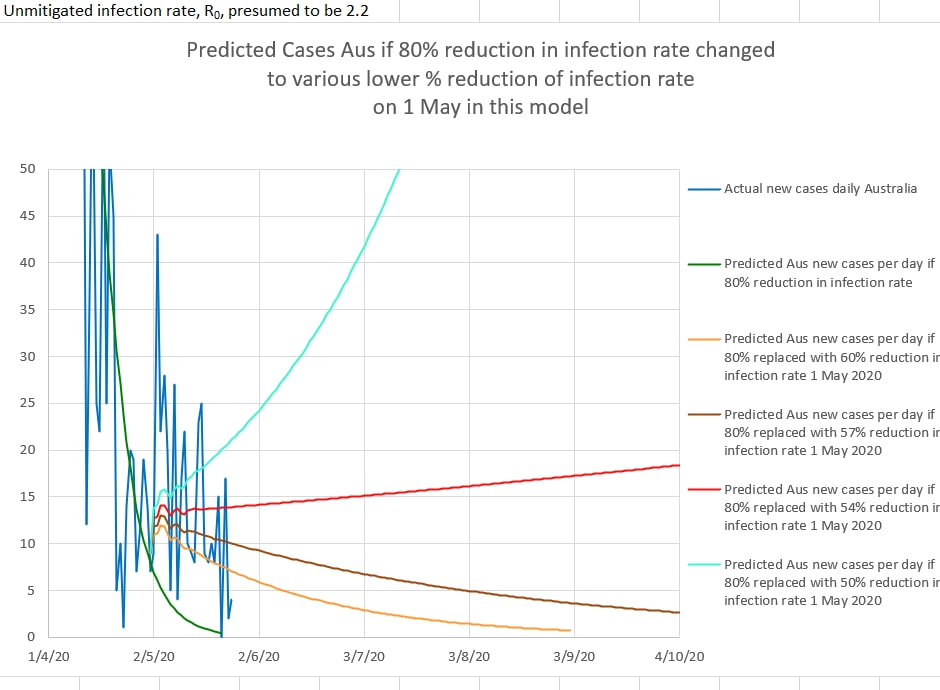
The virus is thought to have an Ro of 2.2 - that is, one infected person infects 2.2 other people on average. The words 'on average' are important. One infected person can, in fact, infect a large number of people depending on the circumstances. For example, in a dormitory, a large family home, a crowded workplace, a crowded family home or a place where a group resides - a single infected person could infect large numbers. Ro is only 2.2 on average. It is almost certainly much greater than 2.2 anywhere where a greater number of people occupy a space for a longer time. So a single case is probably going to infect many others in a dormitory, ship, a workplace where workers must necessarily work close to others or a 'care home' where the space is shared by many. And the others will infect still others and so on. And some of the new infections will be asymptomatic and undetected. It is probably unwise to keep those infected cases, or their contacts, together (in the dormitory, workplace or care home) because the Ro may be considerably higher than 2.2 in those circumstances, and even a 90% mitigation of viral spread will not reduce the Ro adequately. It may be that the best way to deal with a cluster is to nip it in the bud early by removing all the people in question from the space and isolating and monitoring them separately elsewhere. Everyone in a risk prone space should probably be considered a cluster as soon as a single infected person is discovered there. It looked like there might have been trouble brewing a few days ago when there was a rise in new cases per day. Was it a break out of control and a possible start to a second spike? Or was it a spot fire? It looks like it was a spot fire - with delayed detection of a cluster of cases in one workplace. Spot fires are probably to be expected when an epidemic is nearly under control. Each spot fire creates a small spike of its own which subsides as cases are traced and isolated. The graph of new cases a day appears to have returned to the yellow line graphing out the course predicted if the mitigation in place is 80% effective in reducing the infection rate of the virus (from a presumed 2.2 to 0.44). The sudden spike in new cases on 3 May may have suggested that the relaxation of restrictions in NSW on 1 May might have reduced the restrictions efficacy below 50%, which would have signaled a second spike. But those cases probably turned out to be a spot fire and new cases have subsequently safely returned to near the 80% effectiveness of restrictions area of the graph. The Australians, who mainly introduced their own restrictions and isolation well ahead of the Federal Government, and Gladys Berejiklian continue to do a good job.
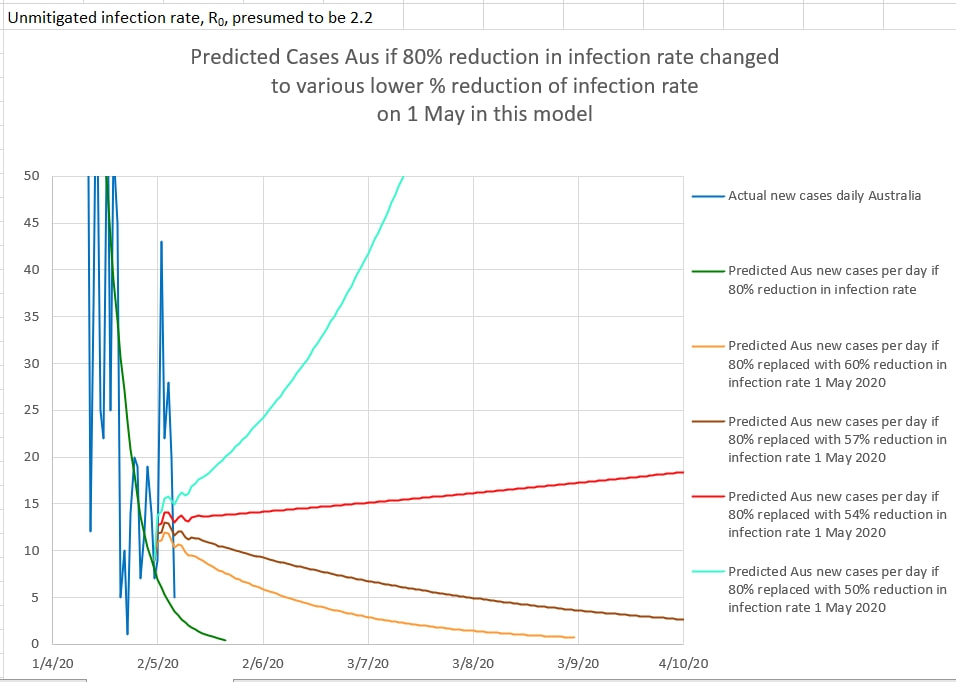
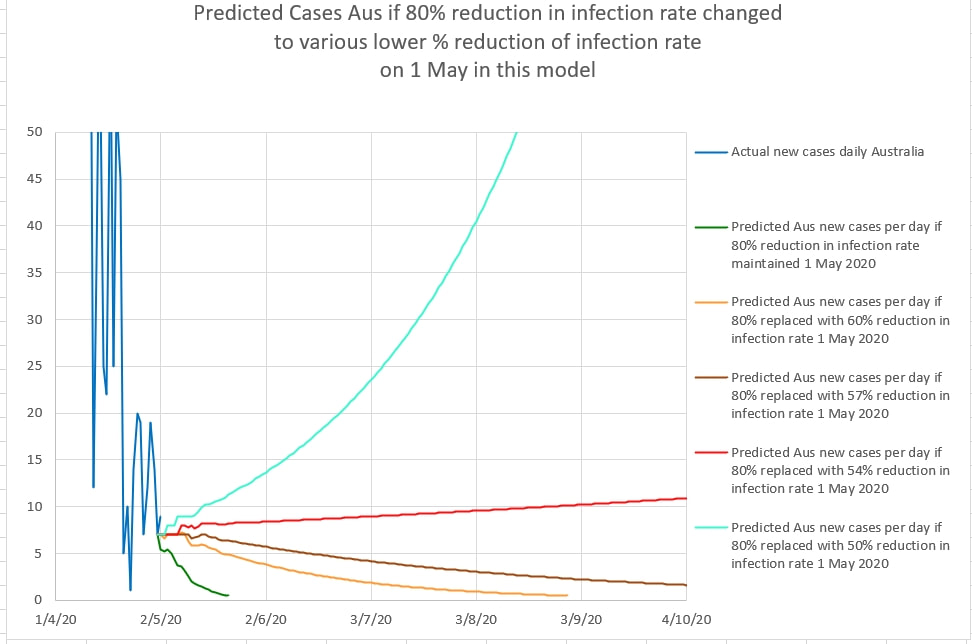
In Australia, NSW started the first stage of gradually lifting restrictions on the 1st May 2020. The change in NSW was that 'two adults and their dependent children' could visit a home. in order to monitor the effect of easing restrictions, the new cases per day can be plotted over a graph of the predicted cases for various percentage of apparent effectiveness of the restrictions. Up until 1st May it appeared that the restriction were about 80% effective in reducing the infection rate of the virus causing Covid_19. The graph below shows the model's predicted daily new cases if the easing of restrictions caused the effectiveness of restriction to reduce to various percentage effectiveness values. The model includes a 14 day logarithmic 'wash-out' of the effectiveness of restrictions from 80% to a lower percentage (each in a separate, coloured graph). The model seems to suggest that the restrictions should remain at at least 60% effectiveness to suppress the virus locally. Slightly less than 60% effectiveness results in a prolonged flat curve, and less than 54% effectiveness results in a significant second spike.
|
AuthorDr Michael Cole FRACP LLB Archives
September 2021
Categories |
 RSS Feed
RSS Feed