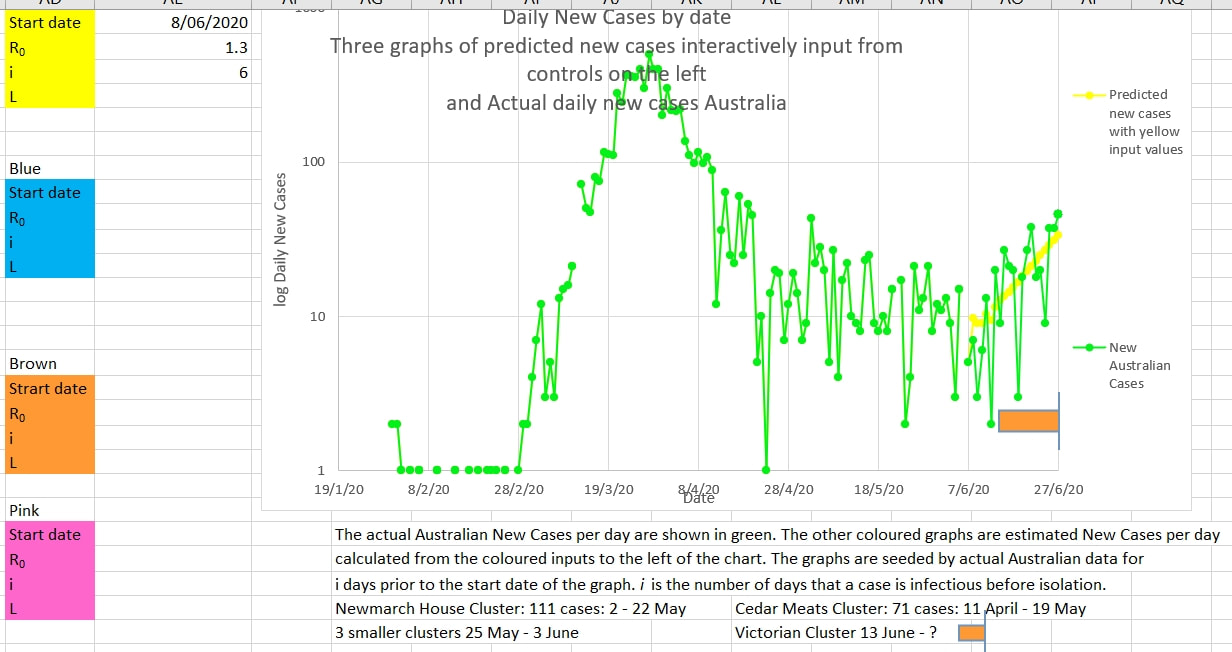
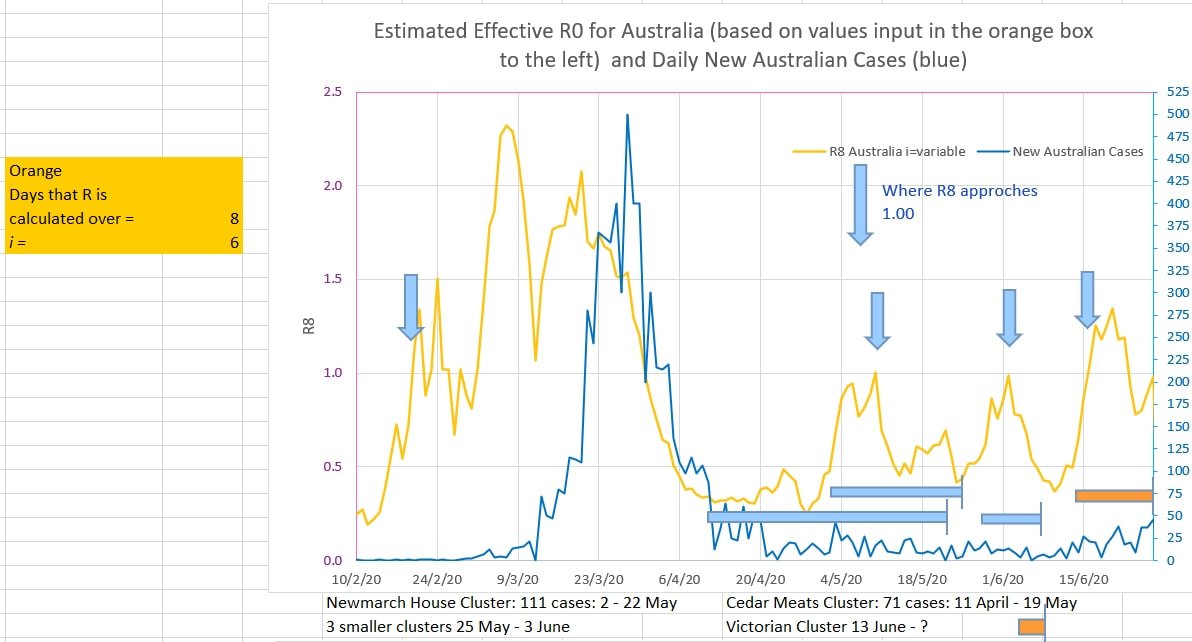
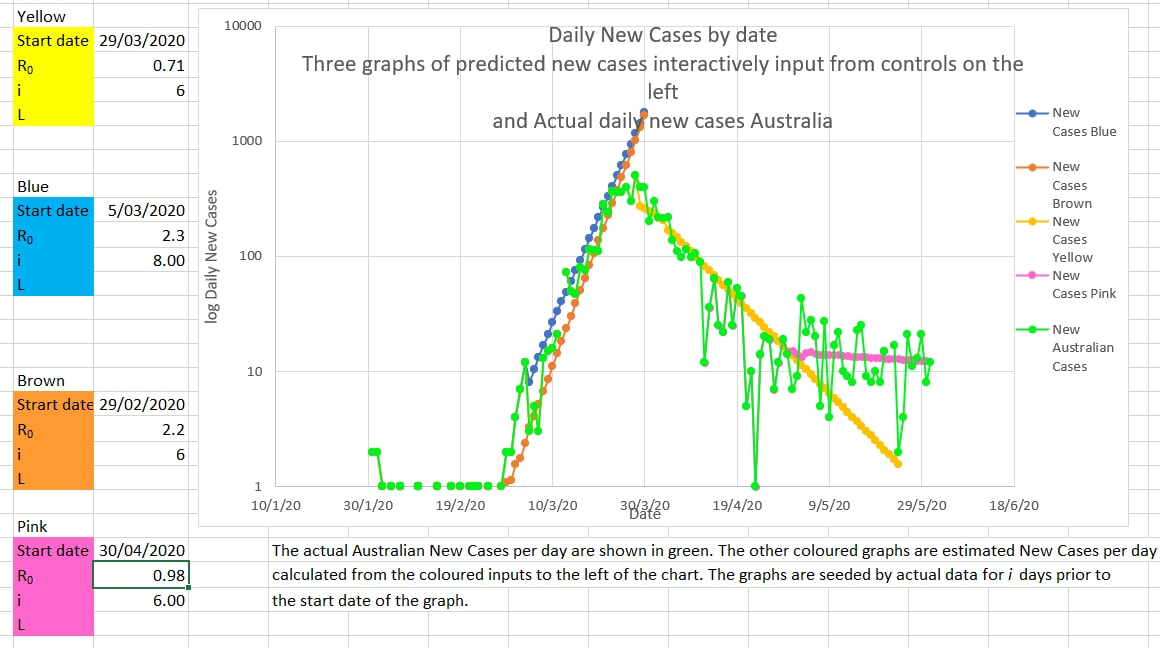
From the graph below it seems that Victoria needs to do more to contain the current cluster. Australia's new cases are plotted in green (log scale). The the yellow graph is 'fitted' to the recent new case (green graph) by trying various values of R0 and i until the slope of the yellow graph approaches the slope of the green graph. The values of R0 and i and are input into the yellow box on the left of the graph. It appears that an R0 of 1.3 and an i if 6 produce a graph that best matches the actual new Australian cases. R0 is the infection rate  (the number of cases infected directly by each infectious person) and i is the number of days that a person is infectious. i may be smaller than otherwise reported because it is the 'number of days that a person is infectious to others in reality' and lasts from when the person becomes infectious until they are detected and isolated; they may remain 'positive' to tests after this but they cease to be 'infectious' in reality because they are isolated or in hospital and not usually able to infect others. An R0 of 1.3 is greater than 1 which means that the spread of infection is increasing exponentially and is 'locally epidemic'. Further restriction need to be put in place to reduce the R0 to less than 1 in Victoria.

The graph below also suggests that Victoria needs to do more to reduce the infection rate, R0. The new cases a day in Australia is shown in the blue graph. The R0 calculated by the model (explained here) is shown in orange. R0 is calculated over a number of days (8 days in this case, and therefore called R8) and for a particular value of i (6 days in this case); These values are input into the orange box to the left of the graph.

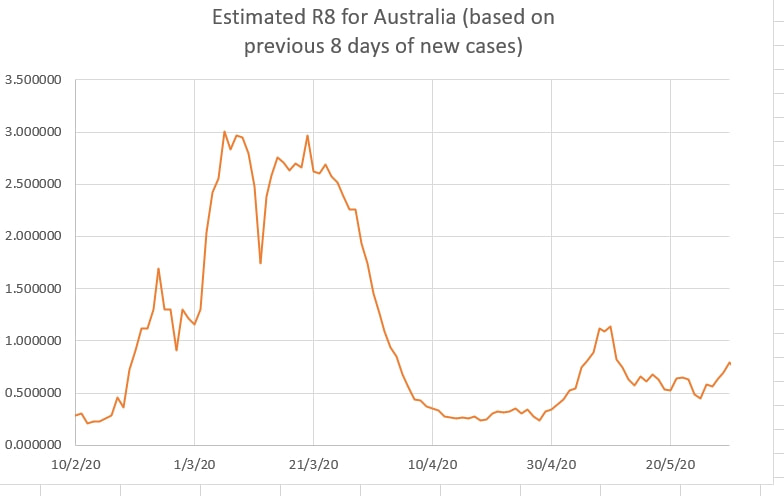
Blue arrows show where the R8 (R0 estimated from new cases over the last 8 days) approaches or exceeds 1 (an exponential infectious rate seen in epidemics).

Since the 13 June 2020 the R8 (R0) has been mainly over 1 showing that tighter restrictions are required to suppress an epidemic rate of rise in cases. R8 also approached 1 at the time of the meat works and the nursing home clusters.

The R8 also exceeded 1 on the 20 February and should have been a red flag warning of an exponential spread of the virus in the population entering Australia and in the population from which they were travelling. It is not probable mathematically for there to be an exponential increase in infection in those entering Australia if there was not already an exponential increase in infection in the population from which they came. That is, the infection was already epidemic in practice (R0 greater than 1) on 20 February, a month before adequate restrictions were put in place. 

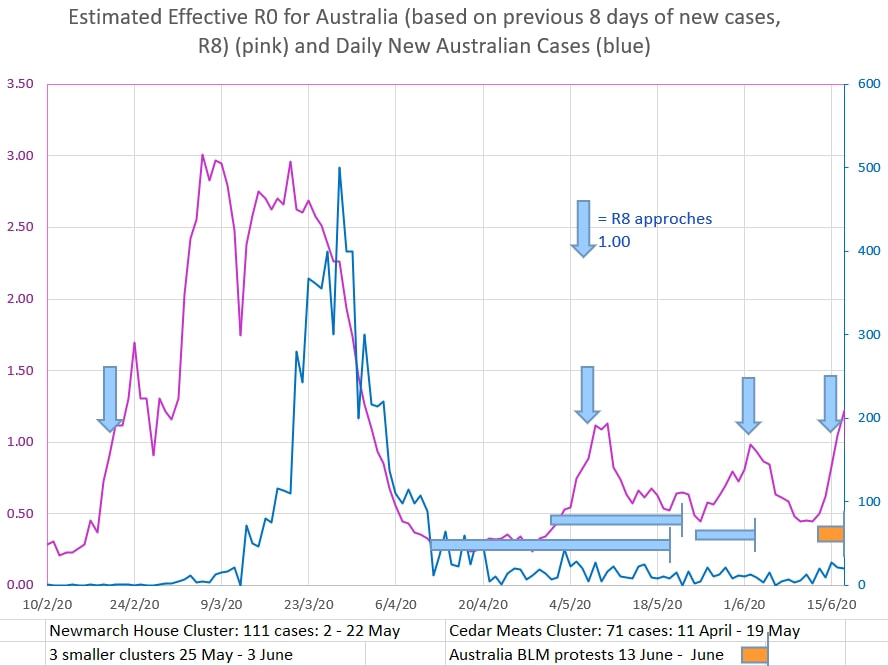
The Black Lives Matter (BLM) protests in Australia were held on and after 13 June 2020.

Many protesters wore masks and some maintained social distancing. Never the less the number of people involved was outside the prescribed limits for gatherings during the viral crisis.

But is there any evidence of a cluster of cases related in time to the demonstrations?

The effective R0 of the virus in the population has been estimated over the previous 8 days (R8) in the pink graph below, using the model here. Arrows mark where R8 neared a value of 1.00 in the past; at the start of the epidemic, for a cluster at a meat works and for a period that had three smaller but almost simultaneous clusters.

R8 appears to have neared and now exceeds slightly 1.00. Potentially this is the start of a new cluster.
(shown by the orange bar).

The graph below shows the new daily Australian cases in green (log axis). For comparison, graphs in pink and yellow have been superimposed using the values for R0 and i input into the boxes to the left of the graph in such a way as to mimic the slope of the Australian new cases graph.. The similar slope of the Australian new cases to the pink graph suggests that the Australian cases were showing an estimated R0 of under 1.00, and the cases were infectious for 6 days on average.

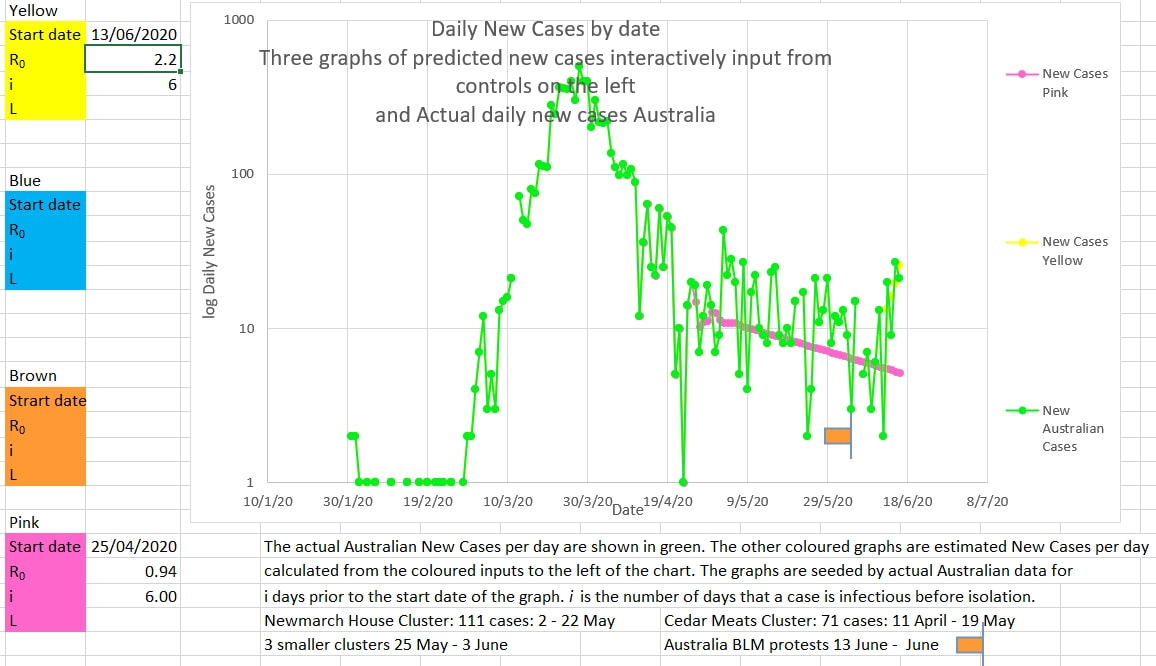
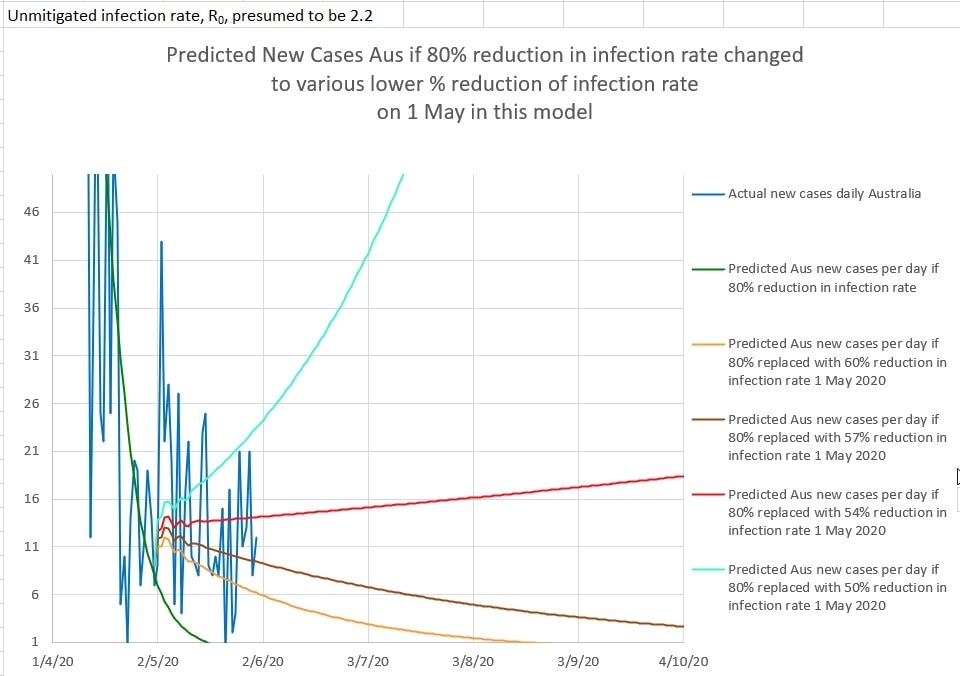
The slope of the yellow graph from 12 June to today suggests the Australian new cases are showing an estimated R0 of 2.2 and that cases are infectious for 6 days on average. However, there are only 5 data points in that series so far; too few to draw any conclusion at all.
​

Since restrictions have been eased in NSW since 1 May 2020  new cases have appeared to increase or decrease randomly each day. The randomness is probably explained by delays and 'catch up' in case reporting and other systemic errors. Until now the trend in daily cases has looked to be downward. But today's graph of New Australian Cases could also be interpreted as steady (the pink graph below). That would mean an effective infection rate, Ro, of near 1. And that would bring Australia close to the start of a second wave.   

The pink graph is the number of new cases a day predicted by the model if the Ro is 0.98 and the number of days a case is infectious is 6 (which is possible since cases are isolated, and infection prevented, soon after they become symptomatic. The pink graph fits reasonably well the actual Australian New Cases a day. 

R8, the effective Ro calculated by the model from the last 8 days of data, appears to be approaching 1. This suggests that vigilance is needed to detect the start of a second wave. 

In the chart above, Australian New Cases per day, in dark blue, are plotted against 4 graphs of predictions of daily new cases if the restrictions since 1 May 2020 were 50%, 54%, 57% and 60% effective.

Critically, the area between 54% effective restrictions and 57% effective restrictions is the difference between a second wave and a steady decrease in cases. The natural day to day error in case reporting makes it difficult to predict in which area, safe or second wave, Australia's cases fall. But it is a close call. So vigilance is required.